The “big data era” of semigroup theory

You probably hate buzzwords as much as I do,  and mathematics is not the first example for data-driven science. We did not set out to do this, but it seems to be happening: our research in semigroup theory gets input/inspiration from the flood of data that computers generate. Computational enumeration started in the 50’s, and now we have SmallSemi for abstract semigroups and SubSemi for various diagram representations. So, what do we do when we have a large data set? Visualising some summarizing features is a good start. So we have enumeration and classification data of several diagram representations, and here are some example images, just to give the taste. Heatmaps, showing the relation between the order of the semigroups and the number of -classes (the local pools of reversibility). First, the subsemigroups of , the degree 3 full transformation monoid. Size versus number of -classes. 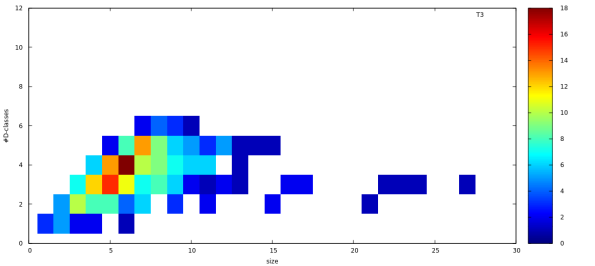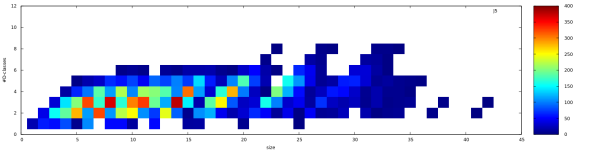Just to observe, order 6 with 4 -classes is the most abundant combination. The Jones monoid of degree 5 seems to be “flat”. 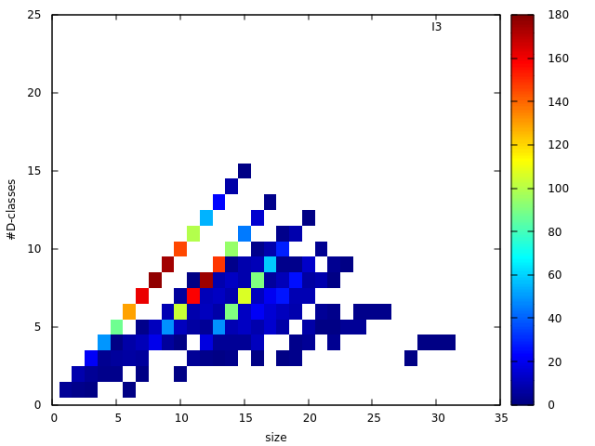While the degree 3 inverse monoid shows a more discretized image. Note the main diagonal indicating that many subsemigroups have only singleton -classes. In contrast, the heatmap looks rather “continuous”. A closer view of the “Shinkanzen”. 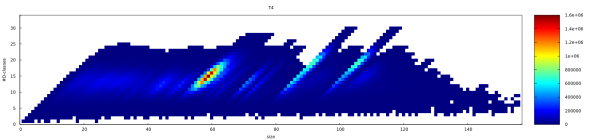These pictures were prepared for EViMS 2, a small workshop on visualisation in mathematical sciences. My conclusion of the workshop was that “Visualisation is not a choice, it is inevitable, even in abstract algebra”. So, more images are coming, hopefully with mathematical explanations.