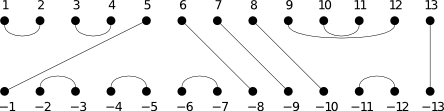The “big data era” of semigroup theory

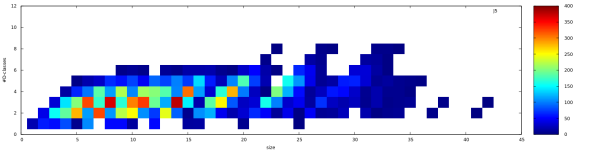
You probably hate buzzwords as much as I do,  and mathematics is not the first example for data-driven science. We did not set out to do this, but it seems to be happening: our research in semigroup theory gets input/inspiration from the flood of data that computers generate. Computational enumeration started in the 50’s, and now we have SmallSemi for abstract semigroups and SubSemi for various diagram representations. So, what do we do when we have a large data set? Visualising some summarizing features is a good start. So we have enumeration and classification data of several diagram representations, and here are some example images, just to give the taste. Heatmaps, showing the relation between the order of the semigroups and the number of -classes (the local pools of reversibility). First, the subsemigroups of , the degree 3 full transformation monoid. Size versus number of -classes. 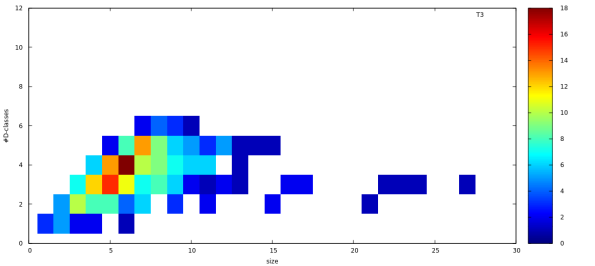Just to observe, order 6 with 4 -classes is the most abundant combination. The Jones monoid of degree 5 seems to be “flat”. 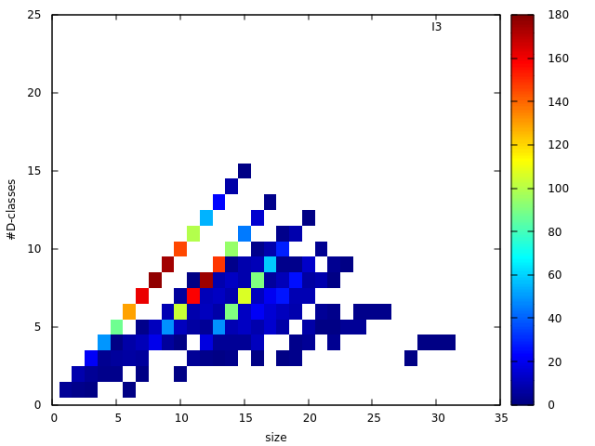While the degree 3 inverse monoid shows a more discretized image. Note the main diagonal indicating that many subsemigroups have only singleton -classes. In contrast, the heatmap looks rather “continuous”. A closer view of the “Shinkanzen”. 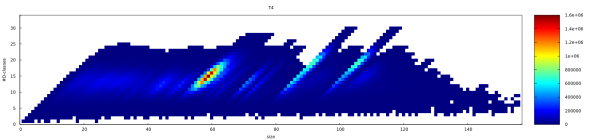These pictures were prepared for EViMS 2, a small workshop on visualisation in mathematical sciences. My conclusion of the workshop was that “Visualisation is not a choice, it is inevitable, even in abstract algebra”. So, more images are coming, hopefully with mathematical explanations.

Organic semigroup theory: ferns growing in the Jones/Temperley-Lieb monoid

What is the interesting part of doing science? When a new idea, or some new technology enable us to see some unexpected connection between seemingly unrelated areas. As the new technology, take the bipartition capabilities of the Semigroups package for GAP, and the related visualisation tools. For the seemingly unrelated fields, take semigroup theory and fractal geometry. Here is the story.

The Jones/Temperley-Lieb monoids are interesting combinatorial representations of semigroups. For degree 4 here are the usual generators:

,     ,       ,      .

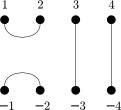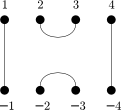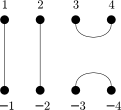Only pairs of dots are connected, and the diagram is planar as a graph. The multiplication is the usual diagram composition, stacking two diagrams, connecting the dots, and doing the simplification if possible. Unlike in diagram algebras, the `bubbles’ in the middle are simply discarded.

Here is a random element of , exhibiting some typical features.

I said `interesting’ before, so I owe you the justification. In mathematics interesting is often equal to difficult. There are a few open questions regarding the combinatorics of the Jones monoid. For instance, one of the basic questions for semigroups is the number of idempotents. By sheer silicon power and coding finesse we can figure out some low degree values (A225798) but we have no formula for that, so beyond our computational horizon it is just darkness.

In semigroups, when you are looking for idempotents, you simply look at the -class picture, and find the -classes with idempotents. Assuming that you have the luxury of having the -class picture in sight. Luckily GAP + Semigroups + VIZ give you exactly that. So Eastie did so. Ok, we still don’t have the closed formula (it probably requires a bit more work than just looking), but he discovered this:

This is a diagram showing the locations of the idempotents in a -class of . Yes, they look like ferns, or more like iterated attempts to get the shape of the fern right ( in the top left corner). And it really looks like those images generated by iterated function systems (repeated affine transformations of a simple geometric object), for example the Barnsley fern.

This image is of course not the first one we saw, by

gap> Splash(DotDClasses(JonesMonoid(9)));

you get something like this:

but when you increase the degree, the generated images eventually choke your PDF-viewer. Also, we wanted to see the images in high-definition, pixel per idempotent precision, so  a little bit of extra coding was needed. The situation is reminiscent of Mandelbrot’s discovery of the Mandlebrot set. The first images were very crude, so they had to sharpen the tools to see them more clearly. Except that in his case he was searching for the set, while for the Jones monoid, James was on his routine patrol.

Needless to say that the image depends on the ordering of the – and -classes, but the algorithm happens to do the right, systematic ordering. Otherwise, the discovery would have been delayed, until someone comes shrewd (or desperate) enough to try reordering.

For the time being, we have no explanation of the ferns growing inside the semigroup structure of the Jones monoid. Knowing that this structure is of interest for physicists, we are wondering about the possible biological connections. In any case, so far we’ve been simply interested in the Jones monoid, but now we are interested and EXCITED! 🙂

Refined classification of the degree 4 transformation semigroups

Previously we classified the degree 4 transformation semigroups by size and by the numbers of Green’s classes. This turned out to be insufficient for finding isomorphic semigroups, so we needed a finer classification. The new property is the number of idempotents, for instance, I016 in the filename means the semigroups in the file all contain 16 idempotents. Furthermore, letter b indicates bands, letter c commutative semigroups, and r stands for regular semigroups.

The size of the archive is around the same, but there are more files in it. 287401 to be precise.

T4SubSgpsConjClassesClassifiedV2.tar.xz

Cycle-trail decomposition for partial permutations

Speaker: James East, Centre for Research in Mathematics, University of Western Sydney

Abstract:
Everyone knows that a permutation can be written as a product of cycles; this is the cycle decomposition. For partial permutations, we also need trails. For example, [1,2,3] means that 1 maps to 2, 2 maps to 3, but 3 is mapped nowhere, and nothing is mapped to 1. Everyone also knows that a permutation can be written as a product of 2-cycles (also known as transpositions). A partial permutation can be written as a product of 2-cycles and 2-trails. The question of when two such products represent the same (partial) permutation leads to consideration of presentations. We give a presentation for the semigroup of all partial permutations of a finite set with respect to the generating set of all 2-cycles and 2-trails. We also give a presentation for the singular part of this semigroup with respect to the generating set of all 2-trails.

There are 132 069 776 transformation semigroups on 4 points…

…and here they are.  If it is not clear why this is so exciting, then this little note may be helpful.

So slightly more than 132 million – up to conjugation, of course. The grand total is 3 161 965 550, but under normal circumstances we are only interested in the conjugacy class representatives.

How do we know? We enumerated all subsemigroups of computationally. It is actually not that difficult, standard search algorithms with some semigroup-specific optimizations, making the search parallel by using Rees-quotients (see draft paper for details). Well, once it’s done, it always looks easy, but it actually took a while (2 years) to finish the calculation. It was a hobby project in the beginning, which became and ‘official’ research project, by the sheer amount of invested time.

The above archive is a bit of a surprise package, the file size is 1.2GB and you need 9.2GB of disk space when uncompressed. The semigroups are classified according to their size and the numbers of , , and -classes. For instance, suppose you are looking for  degree 4 transformation semigroups of size 42 with 6 -classes ,13 -classes and 3  -classes. Then you need to find the file

T4_S042_L006_R013_D003.gens

then you can fire up GAP and the Semigroups package and use the ReadGenerators function to load the semigroups, or rather the generating sets for them. Nice and easy, isn’t it? Well, we are planning to make this a bit more accessible with some web interface magic, hopefully in the near future.

For the above example, the file contains only one semigroup, stored in exactly 42 bytes. 🙂
If the required file doesn’t exist, then there is no degree 4 transformation semigroup with the specified numbers. Or we made a mistake at some point.

Speaking of that, we believe that the archive has no errors and omissions. The enumeration uses simple graph-search algorithms, so the correctness is easy to see. However, with real-world actual physical computers, you can never know. Please let us know if something looks suspicious.

Also lease let us know if you find this database helpful/interesting/exciting/useful.

Here is a talk summarizing the project (in case you can put up with my heavy accent, the audio quality gets better once the mic is switched on).

Building a harvester rig

I decided to build a workstation computer, for several reasons. I have access to many different types of computing resources, with differing advantages and disadvantages. The Nectar Grid for instance provides virtual machines with many cores. Very good for coarse-grained parallel processing, like the case when I have 132 million semigroups in a file and I would like to classify them according to their eggbox pictures. I can divide the file into smaller chunks and using GNU Parallel I can easily utilize all available processors. But for single thread calculations these virtual machines are not ideal since they tend to have older/power efficient slower processors. I’m also fed up with laptops, they are fine for writing code, but once under some load they get hot and burn the battery in an hour. Also, PC building is a dying art and I wanted to have one more go, before it disappears.

For most semigroup and group algorithms the bottleneck is the memory. Orbit calculations, or more generally search trees are not trivially parallelizable. So, the requirements for the new rig:

1. good single-thread performance
2. large memory bank with error correction
3. 24/7 energy efficient operation

One fast processor with huge amount of memory. This is of course totally against the post-Moore’s law era’s trends: many slow cores with little local memory.

Why error correction? RAM modules are quite reliable nowadays, but they do fail sometimes. In most cases the buggy software is blamed, as software failures are more frequent and there is no way to tell the difference between software and hardware failure. But they are rare. So, unless you need very precise calculations that run for days, you don’t need ECC RAM. But that’s exactly what we are doing here, sometimes a week long computation where absolute mathematical precision is required, so not even a single bit-flip caused by a malevolent cosmic ray is allowed. It freaks you out if you start thinking about undetected memory failures. It is a bit like the question whether you want to drive with or without the safety belt.

Choices for the components:

Motherboard: For the Intel 22nm Haswell processors, ASUS P9D WS with the Intel C226 chipset which is meant to be a server chipset (so no overclocking), but the board has some fancy features, like the UEFI BIOS.

Memory: 4x8GB low-voltage, 1600MHz ECC modules. 32GB in total, 16GB per channel.

Power supply: Fanless 400W Platinum (Seasonic). The thought of wasting energy when producing power is simply outrageous. That’s why the premium PSU.

Graphics card: No gaming here.

Storage: Another non-issue. Just use whatever drive I have available at the moment.

Processor: Intel Pentium G3420

No pins here. You have to worry about the motherboard, not the CPU.

What?!?!? A budget processor in ‘high-end’ workstation?!? Well, it is enough for the current purpose. For single thread calculations you don’t need many cores/hyper-threading. This Pentium does support ECC, therefore it is more like a crippled Xeon than a dumbed-down i7. The name ‘Pentium’ is very nostalgic. There is an upgrade path to E3 Xeons, so the build is somewhat future-proof.

After reading Inside Intel this company would be my last choice to buy from, but their products are actually superior. Faster and more power efficient. The full system power consumption is 23W when idling. Not that this value matters, since the machine  is only switched on when there is something to calculate. Half-steam takes 40W, while full blast (both cores using all 4 memory modules) requires 51W. Cooling is not an issue. Unlike my desktop with an AMD FX 8320.

Harvester?!? Well, the expression ‘mining rig’ has been taken by the cryptocurrency folks. Not a big problem since an agricultural metaphor seems better fitting anyway. In most search algorithms we grow trees with enormous foliage in order to get the solutions, the fruits. The truth is that I got the word from the science-fiction movie Moon.

Naming is an important issue. Once we named a subversion server ‘mordor’, and it killed three hard drives in a row. Since the motherboard-memory combination exhibits the Aussie national colors (my current place of residence), the name mollymook came as an obvious choice.

My original idea was not to have a case. Just have the pieces on the table. So I ended up with this:

This of course was a very stupid idea. First, an ATX board is a bit bigger than a Raspberry Pi, second the cables are very rigid, so the above configuration was metastable. A little touch at one point and the components started jumping around.

So, a case was needed. As for housing I’m ok with Scandinavian design. No, ikea hasn’t started selling computers cases yet, but Fractal Design has. It was meant to be a joke, but the furniture company is indeed mentioned in the manual.

Impressive 140mm silent cooling fans.

In a modern case, installing the components and cable-management is easy.

And you end up with a clean build.

For the OS, Ubuntu 14.04 was installed, but this is just an arbitrary choice. For running GAP all you need is a solid UNIX base system and a C-compiler, the details don’t matter.

It is all good, HR mollymook is happily cutting its way through the fabric of the mathematical universe, exploring the unknown, while physically residing in a stylish black&white high airflow box.

Yep, this pseudo-poetic-techno-rubbish metaphor is a good way of ending this buildlog.

The Art of Semigroup Theory

Chances are rare, that you are reading this blog and asking the question: computational what?!? However, you may have some students interested in semigroup theory asking for some introductory material.

Standard textbooks do exist. You can start with Clifford & Preston, Howie, or Grillet, Lallement, Almeida, Eilenberg, etc. But are they available? still in print? Does your library have them? Also, do they cover the latest developments? You may end up using several monographs and some research articles, probably with slightly different notations – heavy burden on the students.

If you are a time-millionaire, then you just compile your own lecture notes. Again, chances are rare…

Alternatively, you search the Internet to check whether someone else had the time. The main idea of using the network is to promote communication and sharing and not to waste efforts on doing something that is already available. So, I searched and found this:

M431 Semigroups  Nine Chapters on the Semigroup Art

The typesetting is beautiful, both printing and ebook readers are catered for…

…and the content aims to be comprehensive. Here are the chapters.

1. Elementary semigroup theory
2. Free semigroups & presentations
3. Structure of semigroups
4. Regular semigroups
5. Inverse semigroups
6. Commutative semigroups
7. Finite semigroups
8. Varieties & pseudovarieties
9. Automata & finite semigroups

All good, I happily printed the whole book and started reading it. And then came the bad news. Some parts were flawless but other sections had numerous typos. I complied a list of typos and suggestions and emailed Alan. To my great surprise I received the answer within 24hrs, and not just the answer but a new version with corrections. Also for keeping track of the corrections, version numbers were introduced. This is a very nice situation: he gets feedback and can improve his work, and with a little effort we get the text that we can recommend to our students. Success story.

Since then there were many revisions. Although it is still a work in progress, I highly recommend these lecture notes as introductory material, the book is already in a great shape. More readers would possibly yield more comments and corrections, so we may get sooner a high-quality text, hopefully in print, maybe on a print-on-demand site.

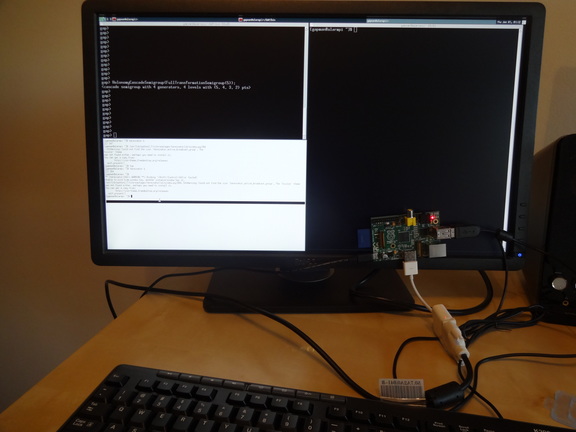
GAP on the Pi

GAP is a system for computational discrete algebra… but I probably should not spend too much time introducing it. Either you know it very well, or you can get all the information from here. I work with it and develop for it every day.  One good thing about it that its kernel is written in standard C, so it is easy to get it working on many different systems.

Raspberry Pi is a little computer that invokes 10% of the feeling of the good old days in the 8-bit era. If you think 10% is a low value, well, today’s computers give 0.1% of the inspiration we experienced back then in 80’s early 90’s, so comparatively Raspberry Pi is doing very well. Again, no need to introduce it. In case you haven’t heard of it, then it is time to catch up. Here or here.

I ordered two of these without knowing what to do with them. One I gave away as a gift, the second one I tried it as a media center. Spectacular success, though my friends were not so excited. The general opinion was that it did not matter on what sort of gadget we watched the movie… Hm, I simply don’t understand people… 🙂

So as a next step I put Arch Linux on it. When I got to the command line (few seconds) I realized that GAP was missing. It takes 106 minutes to compile it form source (mainly because of the GMP library) but then, of course, it works nicely.

Later I got carried away and installed the GUI packages as well.

Here is the Raspberry Pi calculating the holonomy decomposition of the full transformation semigroup on 5 points. As a nontrivial but very simple exercise.

Yes, nontrivial calculations require all the processor power, but the chip does not get too hot. Without any cooling…  It is not fast, but requires little power.

Why doing this? Certainly not for the performance gain. Heavy mathematical calculations are really slow on the Pi, but that is exactly the point. When testing new algorithms it is easier to detect performance bottlenecks on a slower machine. We get lazy on big rigs and don’t produce quality code, unlike in the 8-bit era, where lousy programming yielded no result at all. So, if your algorithm works on the Pi then it will not waste kilowatts on the research cluster.

Also, we develop mathematical software and produce mathematical results eventually used in proofs. Computer calculated results have to be checked carefully. Ideally, given an algorithm we would implement it on two different platforms, using different programming languages developed by two independent teams. That is a luxury we simply cannot afford. However, Raspberry Pi provides us the possibility to test the code on a different architecture at least.

Now I’m checking the availability of a C compiler for our washing machine… 😉

UPDATE: I sometimes use this system for software development. Due to its minimality, it is distraction-free.

Computing Partition Monoids – 3 weeks down under

First of all, we have some name clashes, simply because now there are many persons named James in semigroup theory. So to get this right, here are the names appearing in this story, in alphabetical order:

• JE James East, University of Western Sydney
• ENA Attila Egri-Nagy, University of Western Sydney
• JDM James D. Mitchell, University of St Andrews

Pictorially:

This is a story of the latest development of the Semigroups package, but let’s put things into perspective.

In 2004 JDM inherited the Monoid package with the task of turning it into a GAP4 package as it was originally developed for GAP3. This was done, but after that he became unsure whether it was worth investing more time into the development. He felt that there was not much interest.

In 2010 ENA went St Andrews, determined to squeeze out a release from JDM with some new features needed for SgpDec. One man crowd with banners WE LIKE, WE NEED MONOID! RELEASE EARLY! RELEASE OFTEN! Apparently, this was convincing. JDM started to revise the code.

Around this time Monoid was renamed to Citrus. Much to the excitement then later disappointment for orange growers in Florida.

In 2011 JDM came to Eger, Hungary for the cute little algebra conference A^3. He started to write code for SgpDec and consequently making more upstream changes in Citrus.

Here comes the key point in this story. When including new code for partial permutations JDM was faced with a huge amount of copypaste-then-change-a-bit code. This did not feel right. There was an obvious need for more abstract code, meaning that most algorithms for transformation semigroups work for other semigroups as well. This is a very important moment for computational mathematics, as it is a prime example showing that math and computing is not a one-way relationship. Insights in software development can lead to more abstract and cleaner mathematical descriptions.

In 2012 the BIOMICS project started and they got the idea that inviting two developers is twice as good as inviting one, so JDM and ENA again had an opportunity to work together  again (hinting the general semigroup action framework),  again and again.

But it is time for JE appear on the scene. He and JDM met in Portugal (not for the first time) and talked about partition monoids. These are very interesting structures but without any efficient transformation representation, so these are objects that can really put the general framework to test. JDM in his energetic way did some coding to implement partition monoids in Semigroups, but more consultation was needed. This was not so easy since JE and JDM normally live at the other ends of the world.

In 2013, at the University of Western Sydney a new research centre for Mathematics (called CRM) was formed. The Centre have a program for inviting distinguished international visitors to work with UWS researchers. The more people the visitor can work with the better. JDM was an obvious candidate, and the visit did indeed happen between June 30-July22.

We took over the small meeting room for two weeks. Algorithms were discussed and tried on the board first. The whiteboard space was very limited, but nowadays you just take a shot with your mobile phone and erase the board.

Then the algorithms were immediately turned into GAP functions and methods and tested against the hand-calculated examples and known mathematical results.

JDM’s original estimate was one week, but it actually took 2 weeks to get some tangible results. As software development goes, the estimate was surprisingly accurate.

One example of these new computational results was the D-class picture of the full partition/Brauer monoids. Something that human eyes had never seen before. All in good timing for doing some marketing at the GAIA conference further down in Melbourne. JE gave a talk featuring these new images and there was also a backstage software demo for potential `customers’.

At GAIA we also observed something which must be a generational issue. We got the impression that not long ago mathematicians wrote and sang songs at conferences. What do we do now when we go back to the hotel room? We write code. 🙂 Also, the last row in the lecture room is not used for sleeping any more, it is used for software development. This is of course just an observation, not a judgement, but it seems that academic life was a wee bit more relaxed before.

All in all, as one can see in bitbucket commit messages and in the upcoming preprints, this was a very productive research visit and we also had time for some travel and bushwalks. Maybe a bit taxing on the families, but hopefully the 3 weeks of geek-life will be forgiven.

2013 GAP-SEMIGROUPS-SGPDEC (rainy) Summer Code Camp

Hatfield again, same people. Still BIOMICS funded. Many things happened at high speed. Both on the software and on the mathware side. Also, antisocial geek behaviour reached new heights, for instance sitting down at the dinner table, opening the laptop and telling the others “You may talk to me, but anything not code and math-related will be ignored…”

So, what is the progress?

We did beta testing of James’ development branch of GAP. The novelty here is that calculating with transformations now done in the kernel, which means SPEED!!! increase in every functions using transformations. Of course, having stuff in the kernel implies chasing nasty segmentation faults… but there was a happy end. So the new code is on the way to be included in the upcoming GAP 4.7.

Hand in hand with the new GAP release the semigroup packages are also updated. Citrus got renamed (again), the package is called Semigroups now, less fancy name, but more telltale. Saving future disappointments of orange farmers from Florida. Smallsemi was also hit by the wind of change, duplicate definitions had to be removed.

Following all these upstream changes, SgpDec also got its fair share of commits. Good things: the 0.7 development branch now has all the features of the old 0.6 branch. Everything is back, including holonomy decomposition. Bad thing: except some comments in the testfiles the package is completely devoid of any documentation. Something that will soon be rectified.

Talking of holonomy. We still believe in a short and elementary description of the proof. Working backwards from the working code, this will be part of the documentation.

We also agreed on how to make the one-line notation for finite transformations more compact. It is now called the compact notation.

Regarding the extreme programming part, the 8.5 hours long coding session in a cafe in Hatfield’s Galleria was… hm.. long. At the end of the day we cleaned up the datatypes in SgpDec. So it was very successful, discounting those lost three hours. The trouble came from the combination of these two mistakes:

1. I kept the test files separately, so James could not use them.
2. James continued where he finished in February, but “change as many things as possible at the same time” works fine in the beginning of the development, when everything is broken, but not when the codebase already has some consistency.

Reconciliation was successful. There are now proper test files for SgpDec and we also found those two swapped arguments that caused havoc everywhere.

Some photos:

 
Vertical screen space is important. We like WQHD monitors.

Code recycling – just bring your unused subroutines!

or

James does not produce trash code!

or

Code! if you have 5 minutes to spare…

 

Still thinking about the holonomy decomposition…

Checking the semantics of the compact notation.